User Tools
Page Contents
Expressions and Tables
Some material keywords take not only plain numbers as their parameters, but entire mathematical expressions that are evaluated whenever the material is employed for rendering. Expressions in turn may refer to look-up tables, which are a very simple but flexible means to approximate arbitrary mathemathical functions.
This section explains the details of expressions and tables.
Expressions
Some of the above keywords cannot only take numbers as their arguments, but entire mathematical expressions. An expression is a combination of numbers, mathematical operations, symbols, and table look-ups. Here is an example for such an expression:
(1 + sinTable[ time*0.25 + 3 ]) / 2
Unfortunately, there is also bad news: The current parser of the Cafu MatSys is not yet powerful enough to
parse expressions that use operator infix notation like the one above.
Instead of +, -, *, … we therefore have to use explicit prefix notation,
which is much easier to parse. The prefix notation is explained below.
Here is the above example in prefix notation that we have to use until I can improve the parser to support infix notation:
div(add(1, sinTable[ add(mul(time, 0.25), 3) ]), 2)
Expressions are defined recursively as follows:
$numA number.
$varA variable. Please see below for a list of all valid variables.
$table[ $expr ]A table look-up. The value of the table at position$expris returned. The details of the look-up depend on the tables definition. The default tablessinTableandcosTableare always predefined. Custom tables can be defined as described in subsection Tables. Note that table look-ups are normalized. That is, all table elements are accessed by indices between 0.0 and 1.0, that is, the fractional part of$expr.
add($expr1, $expr2)Adds the results of$expr1and$expr2.
sub($expr1, $expr2)Subtracts the results of$expr1and$expr2.
mul($expr1, $expr2)Multiplies the results of$expr1and$expr2.
div($expr1, $expr2)Divides the results of$expr1and$expr2if$expr2is not 0. Otherwise, this evaluates to 0.
The following variables are defined:
timeThe current system time in seconds, starting from zero.
ambientLightRedambientLightGreenambientLightBlueThe Cafu engine provides the color of the ambient light that is contributed by radiosity light sources in these variables. Therefore, almost all material definitions that are employed with entities (e.g. player models, weapon and item models, etc.) normally use these variables so that the entity is colored according to the ambient radiosity light. Please see the.cmatfiles inGames/DeathMatch/Materials/Models/for many examples.
Tables and table look-ups are described in subsection Tables.
Tables
A special expression is a table look-up of the form $myTable[$indexExpr], where $myTable is the name of a table that must have been defined before use, and $indexExpr is another expression that determines where in $myTable the look-up occurs. The scope of $myTable begins at its definition and ends at the end of the material script.
Here is a simple but complete example with a table of four values:
// This line defines the table "myTestTable":
table myTestTable { { 0.2, 1.4, 0.6, 1 } }
TestMaterialForTableLookup
{
diffusemap someDiffuseMap.png
// ...
rgb div(myTestTable[mul(time, 0.5)], 1.2) // equiv. to: rgb myTestTable[time*0.5]/1.2
}
As you can see, table definitions start with the keyword table, followed by the name of the table.
Then come two { brackets, the table data values separated by commas (arbitrarily many), and then the closing two } brackets.
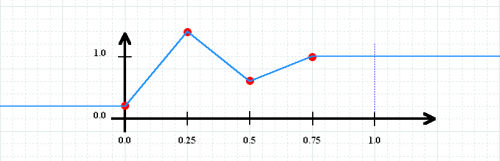
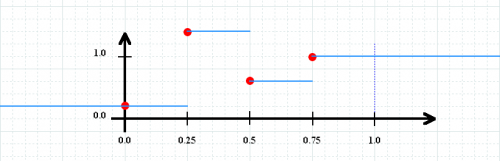
Note that table data values are always mapped into the range 0 to 1. Therefore, the graphical representation of myTestTable looks like this:
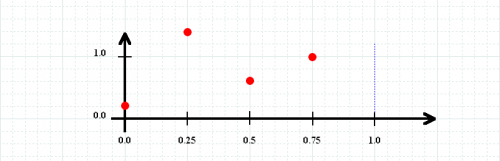
myTestTable[0] yields 0.2, myTestTable[0.25] yields 1.4, and so on…
You may wonder what you get for myTestTable[x] if x is smaller than 0 or greater than 0.75, or what happens if x is “between” two table values. Per default, table values are infinitely repeated outside of the range 0 to 1, and linearly interpolated between two adjacent values. Therefore, myTestTable from the above example in fact represents the following function, graphically shown in light blue color:
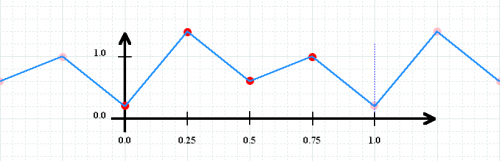 Observe how the values repeat with each integral number. That is, the table in range 0 to 1 is repeated between 1 to 2, between 2 to 3, 3 to 4, and so on. It is also repeated into the negative range, that is from -1 to 0, from -2 to -1, -3 to -2, and so on.
Observe how the values repeat with each integral number. That is, the table in range 0 to 1 is repeated between 1 to 2, between 2 to 3, 3 to 4, and so on. It is also repeated into the negative range, that is from -1 to 0, from -2 to -1, -3 to -2, and so on.
Also observe how intermediate values are linearly interpolated. For example, the value at myTestTable[0.375] (in the mid between 0.25 and 0.5) yields 1.0 as the result.
For example, if you access myTestTable via the MatSys variable time, as in myTestTable[time], then it always takes exactly one second to traverse the entire table. If you want to change the speed with which the table is traversed, then you'll have to multiply the index variable time with an appropriate scale factor. For example, myTestTable[div(time, 3)] will take three seconds to walk the entire table once.
snap and clamp
For special-purpose tables, you can insert the keywords snap and/or clamp between the two opening { brackets of the table definition.
snap turns the linear interpolation off, and instead repeats the previous value until the next table value. Thus, if we changed the definition of our myTestTable above to
table myTestTable { snap { 0.2, 1.4, 0.6, 1 } }
then our graphical representation of the table becomes:
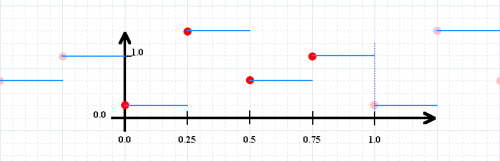
snap turns the interpolation off, and just repeats one value until the next.
Snapping is useful whenever you want to have a table to encode functions that have “hard” rather than “smooth” transitions. For example, in order to have LEDs flicker the SOS morse code, you'd use this table:
table sosTable { snap { 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0 } }
clamp turns off the repetition of the table values outside of the range 0 to 1. That is, adding clamp to our definition of myTestTable yields:
table myTestTable { clamp { 0.2, 1.4, 0.6, 1 } }
With clamp, the first table value is returned for myTestTable[x] where x is less than 0, and the last table value is returned whenever x is greater than 1 (in fact, greater than 1-1/TableSize).
Finally, you can also combine snap and clamp:
table myTestTable { snap clamp { 0.2, 1.4, 0.6, 1 } }
Predefined Tables
Normally, tables must be defined before their first use, but there are also tables that are inherently defined by the MatSys and can always be used without prior definition:
sinTableyields the sinus of its argument. Note that the entire 360° (2pi) arc is compressed into the range 0 to 1, not 0 to 2pi.cosTableyields the cosinus of its argument. Note that the entire 360° (2pi) arc is compressed into the range 0 to 1, not 0 to 2pi.sinTable01likesinTable, but the values are not returned in range -1 to 1, but “compressed” to 0 to 1. That is,sinTable01[x]is equivalent todiv(add(sinTable[x], 1), 2).cosTable01likecosTable, but the values are not returned in range -1 to 1, but “compressed” to 0 to 1. That is,cosTable01[x]is equivalent todiv(add(cosTable[x], 1), 2).